Leetcode 94 - Binary Tree Inorder Traversal （中值遍历）

DocumentsAlgorithms
Algorithms, Leetcode, Python, Tree
Catalogue
  1. 1. Question
  2. 2. Analysis
  3. 3. Code

Question

Given a binary tree, return the inorder traversal of its nodes’ values.

Example:

Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [1,3,2]

Follow up: Recursive solution is trivial, could you do it iteratively?

Analysis

中值遍历是深度优先（Deep-first search）的一种树遍历方式，它先遍历节点左树（左节点），再输出节点自身，然后遍历右树（右节点）。流程如下图所示：

图片来自维基百科

这个问题可以采用递归或循环完成：

  1. 递归
    给递归函数传入一个节点，递归函数再调用自身并传入左子节点，遍历节点左侧；再输出节点自身的值；最后调用自身并传入右子节点，遍历右侧。当前节点为空时，不做处理。

  2. 循环
    循环中需要额外的栈用来储存当前节点下的左节点，当左节点遍历到底时，输出当前左子节点A的值，并将当前节点赋值为其右子节点B。如果右子节点B非空，则从右子节点B开始向下遍历其左子节点C；如果右子节点B为空，则 pop 出 stack 下一个值（即A的父节点）进行输出，然后继续上述循环。这里解释可能不清晰，所以采用字母区别节点，希望代码能够表达清楚思路。

  3. Morris Traversal
    无论是递归还是循环，他们的时间复杂度都是O(n)，空间复杂度都是O(logn)，Morris Traversal 让部分右子节点指回某一级的节点，从而在循环中完成从子节点回到父节点的操作，而不使用额外的栈来储存节点。具体的原理解释不太易懂，这里用图示解释：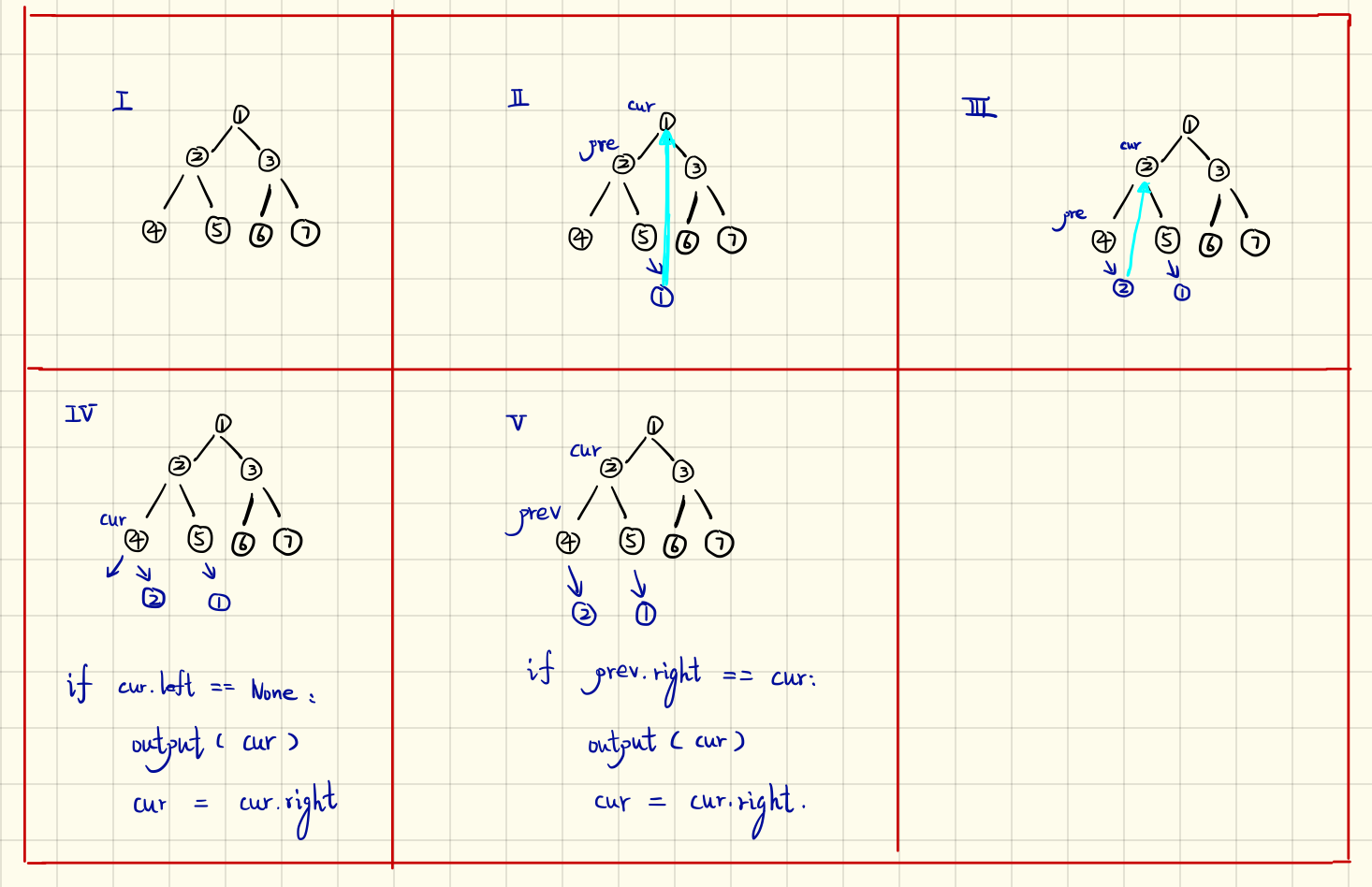
    Morris Traversal

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution:
    def inorderTraversal(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        # Method 1 - Recursive
        # if root == None:
        #     return []
        # res = []
        # self.inorderTraversalHelper(root, res)
        # return res

    # def inorderTraversalHelper(self, root, res):
        # if root:
        #     self.inorderTraversalHelper(root.left, res)
        #     res.append(root.val)
        #     self.inorderTraversalHelper(root.right, res)

        # Method 2 - Iterative
        # if root == None:
        #     return []
        # stack = []
        # res = []
        # while(root!=None or len(stack)!=0):
        #     while(root != None):
        #         stack.append(root)
        #         root = root.left
        #     if(stack):
        #         root = stack.pop()
        #         res.append(root.val)
        #         root = root.right
        # return res
        
        # Method 3 - Morris Traversal
        res = []
        cur = root
        while(cur):
            if cur.left == None:
                res.append(cur.val)
                cur = cur.right
            else:
                pre = cur.left
                while(pre.right != None and pre.right != cur):
                    pre = pre.right
                if pre.right == None:
                    pre.right = cur
                    cur = cur.left
                else:
                    pre.right = None
                    res.append(cur.val)
                    cur = cur.right
        return res
Comments