Leetcode 5 Longest Palindromic Substring （With Manacher's Algorithms)

Documents
Algorithms, Leetcode, Python, String
Catalogue
  1. 1. Question
  2. 2. Analysis
    1. 2.1. 为什么循环嵌套循环，时间复杂度还是 O(n)
  3. 3. Code

Question

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: “babad”
Output: “bab”
Note: “aba” is also a valid answer.

Example 2:

Input: “cbbd”
Output: “bb”

Analysis

回文子串就是字符串当中，正反念都是一样的子字符串，最简单的思路就是先用两个循环遍历所有子串，将每个子串反过来判断是否是回文串，然后找出最长的回文子串，这种方法除了两个循环，判断子串是否是回文串时，也用到了 O(n) 的时间复杂度，所以一共是 $O(n^3)$ 的时间复杂度，明显效率很低。网上还有动态规划的办法，但是效率也不是特别高。普通方法效率不高的主要原因就是重复遍历了一些子串，因此这里直接介绍时间复杂度为 O(n) 的 Manacher’s Algorithms，它借助已有的回文串的信息，减少了重复遍历的次数。

首先，回文串有可能关于中间的一个字符对称（奇数个字符），也有可能关于两个字符间的间隙对称（偶数个字符），因此我们先向每个间隙加入一个分隔字符（这里用”#”），这样所有回文串都会关于一个字符对称，这样做的原因稍后会解释。

接下来会问的问题就是，加了分隔字符后，怎么样从新的字符串中提取原回文串的长度，看下面一个例子。

abcba
01234

#a#b#c#b#a#
012345678910

原回文串的长度为5，加了分隔字符后，长度变为2*5+1，因此原回文串的长度就是新回文串的半径（包括中心）-1。这里是6-1。这样子就可以从新构造的回文串中求得原回文串的长度。接下来介绍，Manacher 如何借助已有的回文串，减少遍历次数。下图展示了一个回文串，假设这是已知边界最右的子回文串，回文串的中心记为 id，右边界记为 maxRight，目前遍历到了 i 处，每个位置的回文串半径用列表 R 储存，途中用红色笔记标出。

Manacher's Algorithms 1

根据 i 的位置，这里需要分情况讨论：

  1. 假设 i 不在最右回文串以内

首先我们使R[i]=1，因为 i 超出了已知回文串的范围，无已有信息可以利用，只能暴力从 i 处开始向两边延伸，判断回文串长度。

  1. 假设 i 在最右回文串以内

我们找出 i 关于 id 对称的点 j (j=2*id-i)，由于回文串的对称性，R[i] 可能等于 R[j]。为什么是可能呢，这里也需要分情况讨论：

  1. j 为中心的回文串超出 id 为中心的回文串

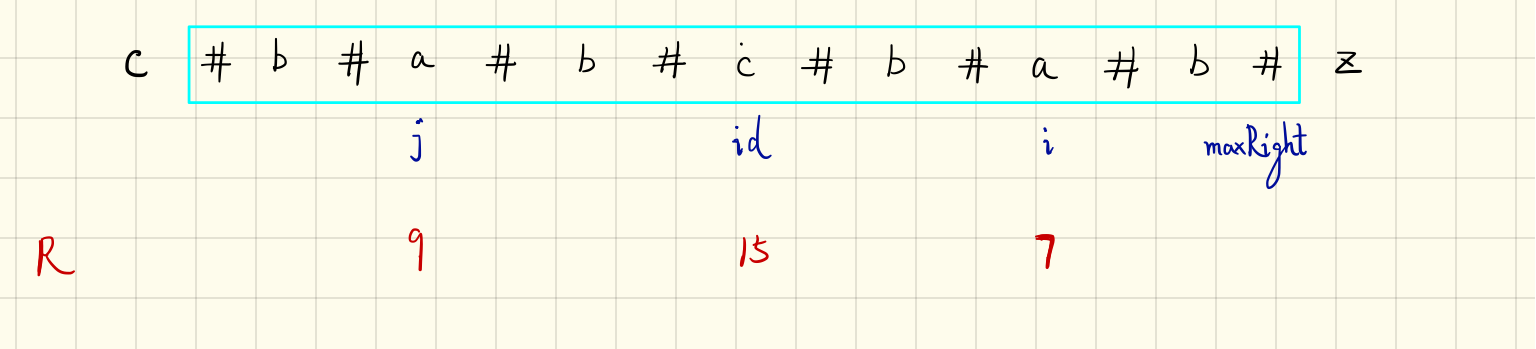
Manacher's Algorithms 2

此时 R[i] == maxRight-id+1，因为这种情况下 i 为中心的字符串不可能超出 id 为中心的字符串。

  1. j 为中心的回文串在 id 为中心的回文串以内

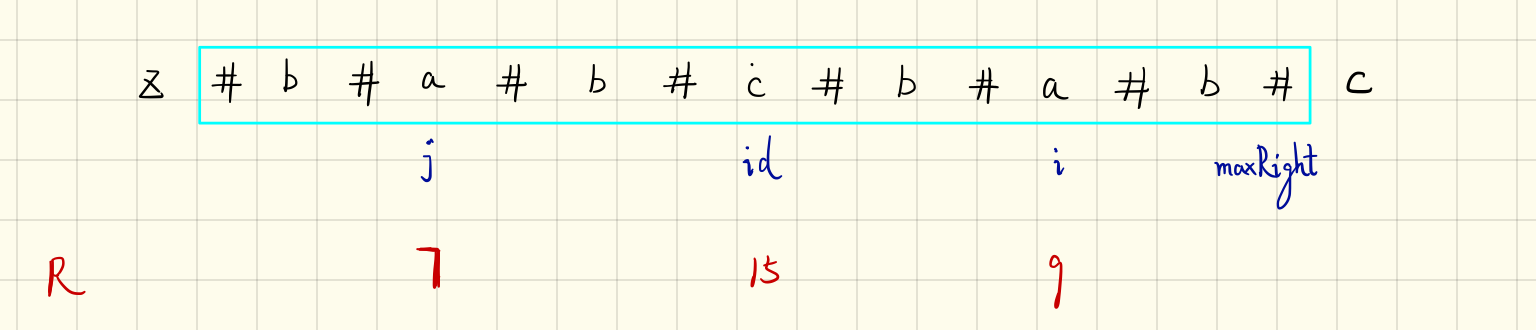
Manacher's Algorithms 3

如果 j 为中心的回文串没有达到 id 为中心的回文串边界，则根据对称性，R[i] == R[j]。反之，先将 R[i] == R[j]，再暴力拓展 i 为中心的回文串，找出回文串的最长范围，因为 i 为中心的回文串可能超出 id 为中心的回文串范围。

至此，R[i] 的值就可以定下来了。然后我们需要更新 maxRight 和 id。如果 i 为中心的回文串超出了原 id 为中心的回文串范围，我们需要将 id 更新为 i, 将 maxRight 更新为 i 为中心的回文串右边界。最后，我们需要得到的 R[i]，更新最长回文串。

Manacher’s Algorithms 十分巧妙地利用已经被发现的最右回文串以及它的对称性，极大的缩短了判断 R[i] 所需要的时间，在一些情况下甚至可以不用暴力寻找回文串就可以确定回文串长度，因此时间复杂度得到很好的优化。

为什么循环嵌套循环，时间复杂度还是 O(n)

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        if s is None or len(s) == 0:
            return ''
        # Preprocessing
        ss = '$#'+'#'.join(s) +'#'  # add boundary
        ssLen = len(ss)
        maxLen = 0
        id = 0
        maxRight = 0
        R = [0]*ssLen

        for i in range(ssLen):
            if i < maxRight:
                R[i] = min(R[2*id-i], maxRight-i)
            else:
                R[i] = 1
            if R[2*id-i] > maxRight-id+1:
                pass
            else:
                while(i-R[i]>=0 and i+R[i] < ssLen and ss[i-R[i]] == ss[i+R[i]]):
                    R[i]+=1
            if R[i] > maxLen:
                maxLen = R[i]
                longestPalinWithSeq = ss[i-R[i]+1:i+R[i]]
            if R[i]+i-1 > maxRight:
                maxRight = R[i]+i-1
                id = i
                longestPalin = longestPalinWithSeq[1:].replace('#','')  # remove boundary
        return longestPalin
Comments